Constructive Cryptography

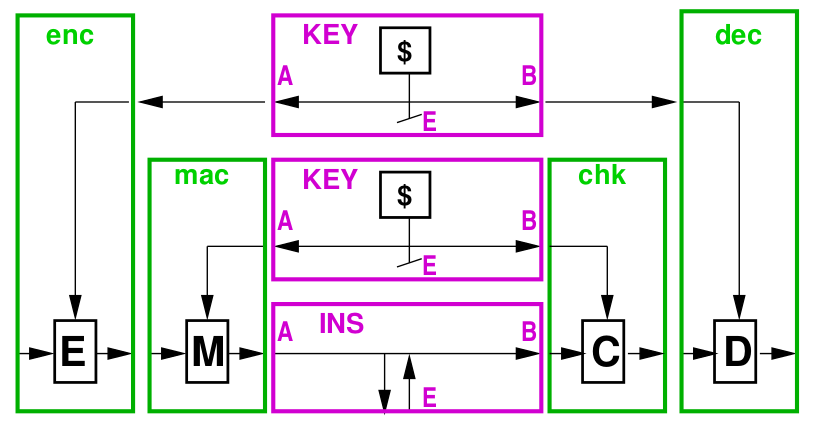
Constructive cryptography is a new paradigm for defining the security of cryptographic schemes such as symmetric encryption, message authentication codes, public-key encryption, key-agreement protocols, and digital signature schemes, and for proving the security of protocols making use of such schemes. Such a cryptographic scheme can be seen (and defined) as constructing a certain resource (e.g. a channel or key) with certain security properties from another (weaker) such resource. For example, a secure encryption scheme constructs a secure channel from an authenticated channel and a secret key.

The term “construct”, which can be defined by the use of a simulator, is composable in the sense that a protocol obtained by the composition of several secure constructive steps is itself secure. This is in contrast to both the traditional, game-based security definitions for cryptographic schemes and the attack-based security definitions used in formal-methods based security research, which are generally not composable.

Constructive cryptography allows to take a new look at cryptography and the design of cryptographic protocols. One can give explicit meaning to various types of game-based security notions of confidentiality, integrity, and malleability, one can design key agreement, secure communication, certification, and other protocols in a modular and composable manner, and one can separate the understanding of what cryptography achieves from the technical security definitions and proofs, which is useful for didactic purposes and protocol design.

Selected Publications

Ueli Maurer and Renato Renner
Abstract cryptography
In Proceedings of Innovations in Computer Science, ICS 2011, pages 1–21. Tsinghua University Press, 2011.

Ueli Maurer
Constructive cryptography—a new paradigm for security definitions and proofs
In Proceedings of Theory of Security and Applications, TOSCA 2011, volume 6993 of Lecture Notes in Computer Science, pages 33–56. Springer, 2012.

Ueli Maurer and Renato Renner
From indifferentiability to constructive cryptography (and back)
In Theory of Cryptography, Proceedings of TCC 2016-B, Part I, volume 9985 of Lecture Notes in Computer Science, pages 3–24. Springer, 2016.