Formalising computational soundness for protocol implementations
Security protocols are distributed algorithms that use cryptography to achieve security objectives. For example, Transport Layer Security (TLS) is used to establish secure communication channels between clients and servers and Internet Protocol Security (IPsec) can be used to set up virtual private networks. These protocols are omnipresent and are used to access and protect numerous applications, ranging from banking to social media. Unfortunately, as history has shown, it is notoriously difficult for protocol designers to correctly design security protocols and for programmers to implement them securely. Numerous protocols, standardized and implemented, have later been successfully attacked and broken.
Contents and Objectives of the Research Project
We envision a collection of tools that supports protocol designers all the way from creating models to prototype implementations. The tools will help ensure that new protocol designs come with security proofs and that reference implementations are correct by construction. Formal guarantees underlying these tools will provide confidence that
the protocols achieve their claimed security goals. In this project, we will focus on the formal foundations to provide such end-to-end security.
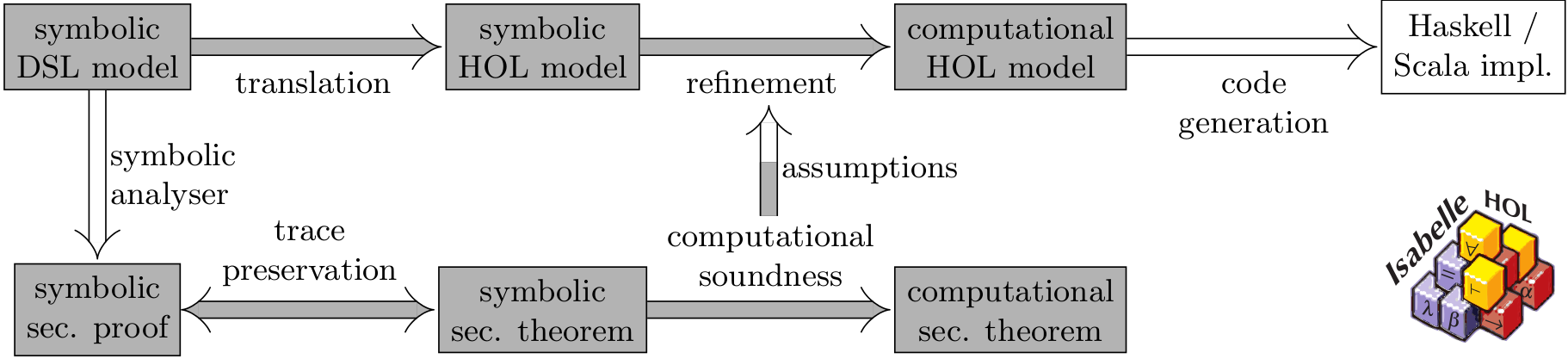
Formal guarantees require a model of the protocol, its desired properties, and the capabilities of possible adversaries. Two kinds of models are well-established: concrete computational models and abstract symbolic models. Computational models are close to real-world implementations, but very technical and far too complex for the average designer or implementor. Conversely, methods and tools for automated security analyses of symbolic models are plentiful and scalable. However, there is a huge gap between the symbolic models and adversaries and real-world implementations and attackers. Computational soundness narrows this gap by connecting the symbolic world with the computational models.
In this project, we will formalise the connection in a proof assistant. This maximises confidence in the correctness, because the proof assistant mechanically checks that all steps are indeed correct and it exposes all assumptions about the protocol and the attacker. This will also provide new insights on computational soundness and the relation between symbolic and computational models.
On the symbolic side, the protocol analysis tool scyther-proof automatically generates security proofs for protocol such that these proofs can be checked mechanically by an independent tool. We will formally connect our formalisation to these proofs to prevent any attacks that could lurk in mismatches in the underlying formal models. Thus, we will get strong computational guarantees with the overheads of symbolic analysis.
Software
You can download the formalisation accompanying the paper Probabilistic functions and cryptographic oracles in higher-order logic by Andreas Lochbihler published at ESOP 2016.
The scyther-Proof tool can be found under http://hackage.haskell.org/package/scyther-proof.
Publications
Andreas Lochbihler
Probabilistic Functions and Cryptographic Oracles in Higher-Order Logic.
In Proceedings of the 25th Symposium on Programming Languages and Systems (ESOP 2016), 2016.
Andreas Lochbihler and Joshua Schneider
Equational Reasoning with Applicative Functors
In Proceedings of the 7th International Conference on Interactive Theorem Proving (ITP 2016), 2016.
Simon Meier and Cas Cremers and David Basin
Strong Invariants for the Efficient Construction of Machine-Checked Protocol Security Proofs
In Proceedings of the 23rd IEEE Computer Security Foundations Symposium (CSF ’10), 2010.
Simon Meier and Cas Cremers and David A. Basin
Efficient Construction of Machine-Checked Symbolic Protocol Security Proofs
In Journal of Computer Security, Vol. 21, no. 1, 2013.
